ベータ値の極限の追求と球状トーラスの最適化
STはどこまで高ベータ化できるか?
ー高ベータ運転にの限界はどこか?ー
小野 靖
(東京大学大学院新領域創成科学研究科)
ONO Yasushi
Graduate School of Frontier Sciences, University of Tokyo, 2-11-16 Yayoi, Bunkyo-ku, Tokyo 113-8656, Japan
High-beta ST research is motivated by its high normalized current Ip/aBT0 achievable at a low aspect ratio and its direct access to second stability for ballooning modes. Key issues for the high-beta ST sustainment are the profile control for ballooning/ current-driven kink stabilities and the positioning of conductive wall for mode suppression. The ST termination by resistive wall modes (RTMRWM) revealed the velocity shear as a tool for the better stability.
Keyword: ST, second stability, ballooning mode, kink mode, toroidal velocity shhear, resistive wall mode
STの高ベータ化は高いI/aBに加え、第2安定化の実現により、炉の磁場設計に大きな余裕を生む。実現のキーは、1)broadな圧力分布とhollowな電流分布の制御によるバルーニングと電流駆動型キンク不安定の抑制、2)導体壁の適切な配置、3)トロイダルシア流の利用である。1)2)は理論解析に実験解析が増えつつある段階、3)は実験を受けて理論解析の段階である。
1. Troyon則が支持する高ベータ化
NSTX(米国)やMAST(英国)等のMA級STが、旧来のトカマクの上限であったトロイダル平均ベータ(用語参照)βT≈10%程度を大幅に越え、トロイダルベータβT≈350%を越すに達する高ベータと0.1秒に及ぶ長い閉じ込め時間tを両立できたしたことは、本格的な高ベータ閉じこめ閉じ込めが現実味を帯びたになったことことを意味する。STがのどこまで高ベータ化できるかの限界は、最も興味ある課題の一つである。
トカマクの安定解析に基づくTroyonのスケーリング則から、限界体積平均ベータ値の大きさは(ただし、cは定数、Iはプラズマ電流、, は体積平均の熱圧力と磁気圧Rは大半径、aは小半径、kは楕円度、qaは端部q値)と表され、アスペクト比R(A=大半径R/a小半径a)を1.5程度まで引き下げると、Fig. 1のように正規化電流が通常トカマクに比べて大きくとれるため、結果として限界ベータ値が大幅に上昇する。これは当初START実験により実証された。さらに、Fig.1の勾配を表す通常のトカマクで3%mT/MA程度である比例定数:規格化ベータbNが、通常のトカマクでは3程度なのに対し、STではFig.1のように倍の6程度まで増加することは要注目である。の高さで説明できない高ベータ特性は、ST特有の新たな高ベータ安定機構機構の存在を意味している。STで使われるは、Bt0が真空磁場のため、常磁性STでは過大、反磁性STでは過小に見積られる。
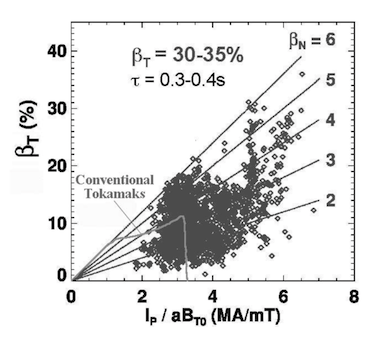
Fig. 1 Toroidal beta βT of NSTX STs and conventional tokamakes as a function of normalized current Ip/aB. The values of Ip/aB and βT are much higher in the STs than those in conventional tokamaks.
2. STで第2安定化が達成可能に
STの限界ベータを考える時、まず考慮すべきはバルーニング不安定であるが、従来の第1安定領域を越えて第2安定領域の超高ベータ状態を達成する可能性がある。局所的な磁場構造と圧力勾配からモード数無限大の理想バルーニングモードの成長を解析すると、不安定領域は縦軸を磁気シアqΨ(=s=dq/dY/q)、横軸を圧力勾配pΨ(=a=dp/dY/p) にをとったs-aダイヤグラム上で表現できる。STと通常トカマクのバルーニング不安定領域は、それぞれFig.2(a),(b)のようになり、その左側は従来の低ベータの第1安定化領域で圧力勾配を大きくするとバルーニング不安定領域に入って配位が崩壊するのに対して、右側下の第2安定領域ではそれがなくなる。トカマクとの大きな差は第1安定領域と第2安定領域の間に窓が生まれることで[1,2]、第1安定領域で低ベータSTを生成した後、適切な分布制御を施しつつ加熱を行なえば、不安定領域を通らずに第2安定領域の超高ベータ状態へ直接遷移できることが判明した。理論解析は、Miller[2]やMenardら[3]が先行し、最近はPaollettiら[4]によりが形状やq分布、圧力分布が形状やバルーニング不安定や低次のバルーニングキンク不安定や電流駆動型を含め、q分布、圧力分布が不安定に与える影響を吟味するなど総合的な解析が行われている。先行する小型実験でもでは高いイオン温度を有するb≈1のFRCに外部トロイダル磁場を加えてFig.2 (a)の曲線Aように第2安定状態の高ベータSTを生成し、ている[5]。これは第2安定状態特有の端部で高い圧力・電流分布勾配と磁気シアとを有するが、曲線Bのように第2安定領域の関係が検討された圧力勾配を下げると不安定領域に入って、配位が崩壊することがわかった[5]。いずれの結果も、圧力分布がbroad、電流分布がhollowとすることが第2安定化の条件であることを示している。さらに窓の大きさ自体も圧力分布がbroad、電流分布がhollowな程、大きくなるため、を示している。担部で急峻な圧力勾配を形成するため端部のq値制御ことが肝要である。
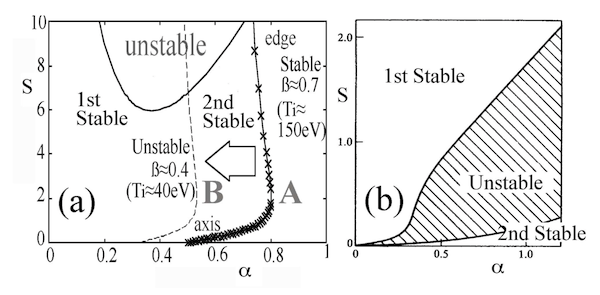
Fig. 2 s-α (qΨ-pΨ) diagrams of (a) high-beta ST (aspect ratio A=1.5) and (b) conventional tokamak (b) . The window between the first and second stable regimes is much wider in the former than that in the latter[5]
3. 超高ベータSTを維持する要件
高ベータSTを安定に維持するキーは、1)圧力・電流分布の適切な制御、2)導体壁の適切な設置、3)シアー流の利用であることが明らかになりつつある。
前節の解析結果を基に、NSTXやMASTでは、高ベータ化、特に第2安定化の達成に向けてなるべく低い内部インダクタンスliを達成して、規格化ベータやトロイダルベータを高める努力を行っている。liの低下は、電流分布をhollowにすることであるを意味する。NSTXの限界規格化ベータβN=5の達成前のもう一つの障害は、hollowな電流分布に起因する電流駆動型キンクモードである。回避するためには、Fig.3のようにliをβNに合わせて上げる必要がある。ただ、導体壁を適切に配置すれば(Mercierモードに考慮が必要なものの)li低下と共にβNを10近くまで上げられる可能性がある。Fig.4はNSTXのモデル計算結果であるが、導体壁が近接しているとバルーニングにもキンクにもベータ限界は導体壁なしの無い場合に比べて3-4割高くなることがわかる。事実、導体壁の遠いMASTではは、βN=5li前後が限界で、βNの最大値5.2(ポロイダルベータβp=2.1,βT=16%,)は壁なし条件下のトロイダルモード数n=1圧力駆動型キンクの安定限界付近にいるである[6]。一方、導体壁の近いNSTXの場合では、βN=10liに達する平坦な分布が生成可能で、壁なし条件の限界ベータを越えたβN=6.5, βp=1.4,βT=35%が達成されたことは特筆に値する。典型的な高ベータ放電のbTや中心q値q0時間変化をFig.5に示す。最大トロイダル磁界の限界から、現状の高βt高βT運転は電流比を大きくとらざるを得ず、Fig.5のようにq0センターq値が1を割る低q運転にならざるを得ずとなるため、トロイダルモード数/ポロイダルコード数が、、1/1の不安定が誘起されて配位崩壊することで、ベータ値の上限が決まっている配位崩壊している。
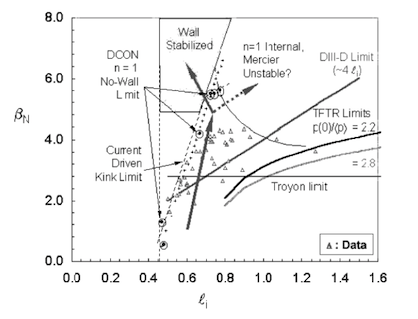
Fig. 3 Normalized Beta beta bN values of NSTX STs as a function of their internal inductance li [7].The beta-limit renewal is being made along two directions with and without wall stabilization.
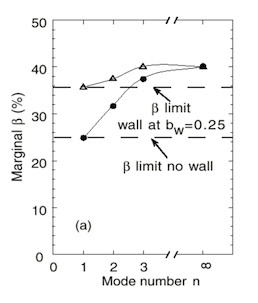
Fig. 4 Marginal beta for kink/ ballooning vs. toroidal mode number n for the no conducting wall case (black circle) and the wall case (triangle) .The maximum beta tends to be higher in the presence of a conformal conducting wall.
4. 速度シア・回転は安定領域を広げる
STで自己発生するアルヴェンベーンマッハ数0.3に達するトロイダルシアー流のが安定化への大きく寄与する点は要注目である[7]。この流れを導入すると、n=1圧力駆動型不安定の成長率が1/3以下に低下するとのMHD計算もあり、実際、NSTXではも大きな速度シアのために不安定が抑制されている。Fig.5でのβT=31%とβT=23%のケースを比較すると、よりように流れの大きなケースでn=1モードは飽和して高いベータ値が達成されていることがわかる。流れが衰えると抵抗性壁モードが発生し、ST配位が崩壊するしている。シアー流が高ベータSTの維持に役立つことが実験的に明らかになりつつあるが、その検討にはMHD解析を越えた運動論的な考慮が不可欠である。実際、NSTXは流れのために密度勾配は磁気軸付近でも有限で、22流体平衡として解釈できそうである[8]。高ベータ領域のSTではこうした22流体、あるいは運動論的な安定性安定化効果が将来的に、高ベータST配位の安定性を確保する有力は将来、高ベータ領域STの安定性を確保する有力ツールと発展する可能性を有しているツールに成長し。一方、、導体壁の利用は、導体壁の磁場浸み込み時間を越えた運転や、より高いモードの抑制に向かうものと考えられる。その延長線上にはneural-net的なコイル群の電流制御に発展する可能性もある。こうした先進的高ベータ不安定制御は、これからのST研究のフロンティアに成長するもの可能性を秘めていると期待される。
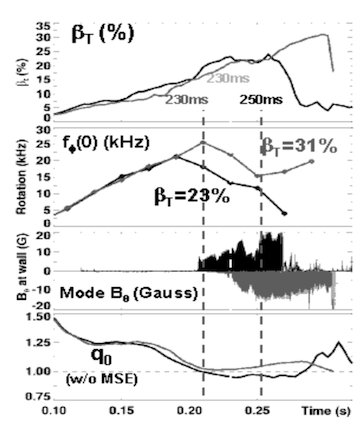
Fig. 5 Normalized Beta bN values of NSTX STs as a function of their internal inductance liTime evolutions of toroidal betasβT, toroidal rotation frequencies ff , mode amplitudes BQ at wall and center q values q0 for high-beta (βT=31%) and low-beta (βT=23%) ST discharges [7].
5. 絶対極小磁場を持つ超高ベータ合体生成で限界突破
異極性合体を用いてトロイダル磁気エネルギーをプラズマ加熱に寄与させることによって、ポロイダルベータ>1の超高ベータ状態の形成が可能と考えられる が、異極性合体においては合体する二つのトーラスプラズマが互いに逆向きのトロイダル磁場を有している必要があるため、二つのプラズマを取り巻く外部コイ ルによる準定常トロイダル磁場の下で異極性合体を実現することはできない。そこで、ポロイダルベータ>1の超高ベータSTの形成手段として、ス フェロマック異極性合体を行った後に速やかに外部トロイダル磁場を立ち上げるという方法が提案されている[9]。TS-3実験では、Fig. 6 に示すように、異極性合体時の磁気リコネクションによって150eVを超える急速イオン加熱が実現されており、その後に外部トロイダル磁場を立ち上げるこ とによってST配位への遷移を行っている[9-11]。このようにして生成された超高ベータSTのトロイダル電流密度およびトロイダル磁場の径方向分布 をFig. 7 (a)(b)に、合体を用いない低ベータSTのトロイダル電流密度およびトロイダル磁場の径方向分布をFig. 8 (c)(d)に示す[10]。この超高ベータ状態では、異極性合体による大きな加熱効果がHollowな電流分布をもたらし、高ベータプラズマに後から外 部トロイダル磁場を印加することによってプラズマ内部に反磁性のトロイダル磁場分布を形成している。これら2つの特徴的な効果の複合によって特にプラズマ 端部付近で大きな圧力勾配が保持されており、結果的に極めて高い(>0.6)トロイダルベータを有するST配位が実現されている。結果として、リコ ネクション加熱により、高ベータ不安定の成長時間以下の短時間(Sweet—Parker時間程度)でいろいろなベータを持つSTを生成することができ た。それをトロイダルベータとI/aBtの空間にプロットするとFig. 7のようになる。ベータが1に近い超高ベータの平衡もあるが、FRCにトロイダル磁場を印加しただけの不安定な状態もあり、多くが不安定である。リコネク ション加熱時間の短さのために不安定な配位も生成可能である点は大きな特徴である[11]。
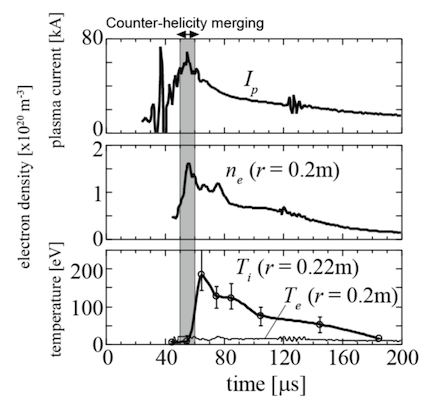
Fig. 6 スフェロマックの異極性合体で生成したFRCにトロイダル磁場を印加して超高ベータSTを生成する過程におけるプラズマ電流Ip (上)と電子密度ne (中央) とイオン温度 Ti と電子温度Te (下) の時間変化 [10].
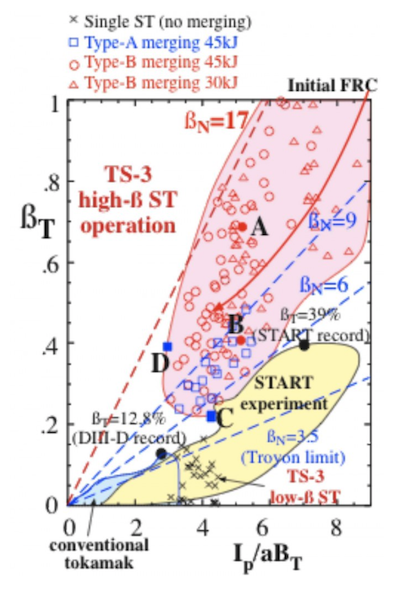
Fig. 7 ST同士の合体生成(Type-A),スフェロマックの異極性合体にトロイダルトロイダル磁場を印加して生成した(Type-B)高ベータSTのトロイダルベータ値のIp/aBT依存性.
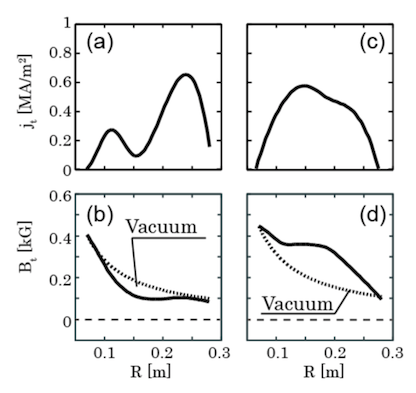
Fig. 8 スフェロマックの異極性合体で生成したFRCにさらにトロイダル磁場を印加して生成した超高ベータSTの(a)トロイダル電流密度jt、(b)トロイダル磁場Btの半径方向分布と、合体なしで単独生成された低ベータSTの (c)トロイダル電流密度jt、(d)トロイダル磁場Btの半径方向分布 。真空トロイダル磁場を点線で表示した[10].
Fig. 9 (a)異極性合体生成FRCにトロイダル磁場を印加して生成した高ベータST (安定:ケース A) と(b) 中クラスベータのST (安定: ケース B) 、STの同極性合体で生成した低ベータのST (安定: case C) と中クラスベータのST (不安定: case D)のqΨ (磁気シア)- pΨ (熱圧力勾配) ダイヤグラムとバルーニングモードに対する第2安定領域。Case A-D はFig. 7 のA-D に対応する[11].
超高ベータでかなり安定なSTも生成され、例えばFig. 9(a) のCase Aは超高ベータながら絶対極小磁場配位を持つ反磁性トカマクである。形成された超高ベータ状態は、バルーニングモードに対する第二安定化領域に位置してい ること[4]に加えて、磁気軸付近における絶対極小磁場構造と、異極性合体に由来するアルベーン速度の50%程度に達するトロイダルシアフローを有してお り、MHD不安定性が抑制されていると考えられる[11]。
Fig. 7に合体生成した高ベータSTのs-α ( qΨ–pΨ) ダイヤグラムを描いてバルーニングモードに対する安定性を解析した例を示す。Fig. 8のCase Aの代表的な磁気面に関する結果がFig. 9上のAであり、明らかに第2安定状態に位置していることがわかる。同様にFig. 7のCase B,C,Dについて解析した結果をやはりFig.9上下に示す。Case Bはベータ40%で不安定な例、Case Cはベータ20%で安定な例、Case Dはベータ40%で不安定な例である。Fig. 9上下を比較すると不安定領域がかなり異なっていることがわかる。これは配位の電流分布などにより大きく変化し、一般に圧力・電流分布の broadnessとhollownessを強めていくと、第1・第2安定領域の間の窓も次第に大きくなるとの興味深い知見が得られている[11]。た だ、こうした分布は電流駆動型モードに対して不安定になりがちで注意を要する。超高ベータ状態の安定性や閉じ込め特性はまだ不明点が多く、例えば、 hollowな電流分布に起因する圧力・電流駆動型の不安定の解析やより詳細なバルーニング不安定の解析などの更なる検証が必要である。現状では同種の実 験は小型装置における短パルス運転に限られているが、今後はより大型の合体実験装置において追加熱による超高ベータ状態の維持を実現することが急務となろ う。
6. まとめ
STの限界ベータの高さは従来のトカマクにはない優れた特性の一つである。ベータ値が上がるほど磁気井戸が深くなる特性は高ベータ配位の安定性を確保する上で有利である、ST炉の磁場設計に大きな余裕を生む40%を越える高ベータ化は、Troyon則が支持する電流・磁場比I/aBの高さに加え、高ベータで最も危険なバルーニングモードに対する第2安定化を達成することにより実現される。実現のキーは、1)broadな圧力分布とhollowな電流分布の制御によるバルーニングと電流駆動型キンク不安定の抑制、2)導体壁の適切な配置、3)トロイダルシア流の利用である。1),2)は理論解析に対し、実験解析が増えつつある段階、3)は実験を受けて理論解析が行われている段階にある。
参考文献
[1] J. M. Greene et al., Nucl. Fusion 21, 453, (1981).
[2] R. L. Miller, et al., Phys. Plasmas 4, 1062, (1997).
[3] J. E. Menard et al., Nucl. Fusion 37, 595, (1997).
[4] F. Paolletti et al. , Nucl. Fusion 42 418, (2002).
[5] Y. Ono et al, Nucl. Fusion 43, 789, (2003).
[6] R. J. Buttery et al., Nucl. FusionFusion Energy Eergy2002 , EX/S1-643, 789, (2003).
[7] J. E. Menard et al., Nucl. Fusion 43, 789330, (2003).
[8] L. C. Steinhauer et al.,, Phys. Rev. Lett. 79, 3423, (1997).
[9] Y. Ono et al, Phys. Plasmas 7, 1863. (2000).
[10]井,小野:「磁場反転配位を用いた超高ベータ球状トカマクの生成実験」プラズマ・核融合学会誌76,553, (2000).
[11] Y. Ono, et. al, Nucl. Fusion 43, 789, (2003).
[12] Y. Ueda and Y. Ono, Nuclear Fusion 41, 981, (2001).
[13] S. Inoue, Y. Ono, et al., to be pulished in Fusion Energy 2012, PD/P8-17 ,(2013).
[14] K. Yamasaki et al., “Electron heating during magnetic reconnection in the UTST merging experiment”, in Proc. 20th International Toki Conference.

