磁力線のつなぎ代わりはプラズマの構造変化を決めるキー!
プラズマ合体が開く磁気リコネクションの世界
— 高ベータ核融合から宇宙まで —
小野 靖(東京大学大学院新領域創成科学研究科)
Laboratory Experiments of Magnetic Reconnection
ONO Yasushi
University of Tokyo, Tokyo 113-8656, Japan
プラズマ核融合学会誌から抜粋
1.はじめに
数年前の太陽観測衛星「ようこう」[1] や地球磁気圏観測衛星「GEOTAIL」[2]の打ち上げにより磁気リコネクション(磁力線再結合)の研究環境は大幅に改善した。太陽コロナでは美しい2 次元X線画像によってリコネクションがプラズマを加熱する様子や、地球磁気圏尾部では速度分布関数の計測が可能となり、リコネクションの役割が広く認識さ れるようになった。しかし、その機構解明となると衛星観測には多くの制約がある。太陽観測衛星は観測対象までの距離が長いため、2次元観測と引き替えに、 1)視線方向の分布の情報がほとんどない、2)局所計測ができない、3)特に肝心のつなぎかわる磁力線がわからない(コロナの足下の磁場のみ)といった問 題がある。地球磁気圏衛星は観測対象の中に入って観測するため、すべてのパラメータが直接観測できるものの、一つの衛星によるピンポイント計測にならざる を得ず、空間的な広がりや分布がわからない。限界を突破するため、どうしても磁気リコネクションの室内実験の必要性がクローズアップされることになる。
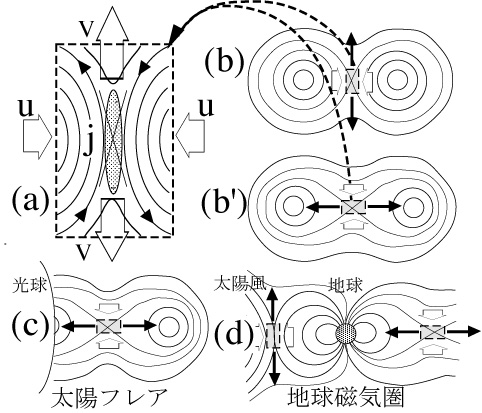
Fig. 1: (a) 2-D slab model of magnetic reconnection and (b) whole configuration of reconnecting field lines
室内プラズマ実験の一つに核融合プラズマ実験がある。確かに計測の自由は大きいが、リコネクション点がプラズマの中に多数存在したり、その局所的な情報がわからないといった問題がある。例えば逆転磁場ピンチ(RFP) におけるリコネクション(ダイナモ)研究では、広く平均化された情報の中にリコネクションの特性を推定するしか無かった。トカマクの鋸歯状波振動は最もリ コネクション研究に貢献したが、局所的な磁力線構造を計測・検証することは難しい。こうした状況で、磁気リコネクションを扱う専用の実験が必要であること は、比較的古く1960年代から指摘されてきた。
2.オープン系およびクローズ系磁気リコネクション室内実験
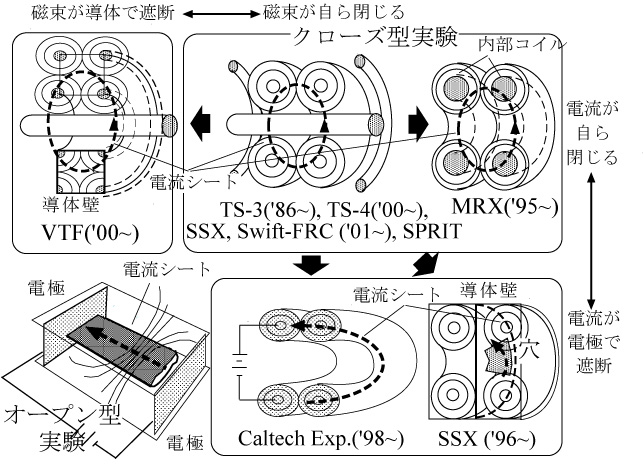
マックスウェル方程式により、すべての磁力線は必ず閉じた形状をしている。図1(b)の磁力線の一部である(a)の四角の部分を便宜的に 切り出す理論モデルやシミュレーションと異なり、実験ではすべての磁力線を決める必要がある。1990年までに試みられてきた磁気リコネクション専用実験 は極めて少数である。多くの場合、電流シートを電極放電で模擬し、図2左下のように、上下の導体板に流す電流で反平行の磁力線を作り、電極放電により電流 シートを形成する。図1(a)の四角の領域をなるべくそのまま模擬するもので、電流シートが開いた形をしているので「オープン系」リコネクション実験と呼 ぶ。日本の大薮らの先駆的な実験[3]、米国でもStenzel, Gekelman[4]らの実験、ロシアではFrank[5]らの実験が広く知られている。Stenzelらは、リコネクションの電流シートのティアリン グ不安定やリコネクションに伴う流速や加熱などの興味ある物理を明らかにした。この方式は制御性が優れるものの、電流シートが外部回路とつながるため、電 流シート内の電界、即ち磁気リコネクション速度に影響がでてしまう。電流シートや磁場が容器や電極に接合する等、境界条件に問題が大きかった。
磁 気リコネクション専用実験が少なかった理由は、1)X点を含む開いた磁場構造のため、高い磁気レイノルズ数、温度、密度を確保できない、2)開いた磁場構 造を切り出して実験すると境界条件の設定が難しい、3)ダイナミックなリコネクションを進行させつつ、系全体を安定に保つことが難しい、4)小さな領域で 多次元で進行するリコネクションを捉える多次元計測が難しい等である。これに対して、図2中央上 のようにトカマク、あるいはスフェロマックといったトーラスプラズマを軸対称合体させ、接合面でトロイダル方向に閉じた電流シートが自発的に形成する「ク ローズ系」の磁気リコネクション実験が開発された[6]。この手法の利点は、1)系が閉じた形状をしているため、電流シートが自発的に形成される、2)磁 力線の一部を切り出さずに、境界条件に問題のない閉じた磁力線全体を取り扱う、3)プラズマ閉じ込め能力を持つトーラスプラズマを用いるので、ある程度の 温度、密度、磁気レイノルズ数が確保しやすいなどである。ただ、電流シート形成も合体も自発的に起こるので、傾斜モードなど不安定に対する配慮が必要であ る。
Fig. 2: Family of magnetic reconnection experiments under operation.
この手法は、東京大学TS-3(Tokyo University Spherical Torus No. 3)装置のプラズマ合体実験[6]が先駆けとなって、その後、1995年にプリンストン大学MRX(Magnetic Reconnection eXperiment)装置[7]、1996年にはスワルスモア大学SSX (Swarthmore Sphreromak eXperiment)装置[8]、1999年マサチュセッツ工科大学VTF(Versatile Toroidal Facility)装置[9]、2000年にはNASAマーシャルスペースセンターのSwift-FRC装置[10]、Caltechの新装置[11]、 東京大学TS-4[12]など、プラズマ合体を利用した磁気リコネクション実験装置の建設が相次いでいる。これらの装置の概念図を図2に示す。これらは相互に似通っているが、比較すると境界条件が異なることは注意を要する。TS-3やTS-4装置がコイル等から完全に切り離されたトカマクやスフェロマックやRFPを2つ自発的に合体させる自由境界条件を用いるのに対して、MRX装置はコイルの周囲にスフェレータプラズマを生成・合体する形式で、コイルが誘導電界を印加する半固定境界条件となっている。VTF装置は電流シートこそ閉じているが、磁力線はXポイント付近を四角に切り出した固定境界条件を用いており、磁力線が導体に遮られる点は現存のオープン型の実験CS-3Dと大差がない。SSX、Swift-FRC、SPIRITはTS- 3/4と極めてよく似た自由境界実験であり、特に後者2つはスフェロマック合体によるFRC生成のみに特化した装置として、それぞれ建設中、提案中であ る。SSXはFRC生成以外に局所的なリコネクションを実現するため、2つのスフェロマックの間に穴の空いた導体壁をおくオープン型実験とよく似た実験も計画している。
Table 1: Laboratory experiments of magnetic reconnection under operation
| Device | CS-3D | TS-3 | MRX | SSX | TS-4 | VTF | Swift-FRC | SPIRIT |
| Institute | G. Phys. Inst. | U.Tokyo | PPPL | Swarthmore C. | U.Tokyo | MIT | NASA | PPPL |
| Construction | 1975 | 1985 | 1995 | 1996 | 2000 | 2000 | Under const. | proposal |
| Method | Open | Merging tokamak/ spheromak/ RFP | Merging spherator/ spheromak, | Merging spheromak, | Merging tokamak/
Spheromak/ RFP |
Merging cusp | Merging spheromak, | Merging spheromak, |
| Major Radius | 20cm | 35cm | 20cm | 50cm | 100cm | 20cm | 40cm | |
| Boundary Conditions | Open Current
Open Flux |
Closed Current
Closed Flux |
Closed Current
Closed Flux |
Open (or Closed) Current
Closed Flux |
Closed Current
Closed Flux |
Closed Current
Open Flux |
Closed Current
Closed Flux |
Closed Current
Closed Flux |
| Te[eV] | 5-150 | 10-40 | 3-20 | 20 | ? | 15-25 | ? | ? |
| Ti[eV] | 5-300 | 10-200 | 3-20 | 20 | ? | 0.2-10 | ? | ? |
| ne [m-3] | 1-10×1022 | 1-50×1019 | 1-50×1019 | 1019 | 0.5-10×1019 | 0-2×1017 | ? | ? |
| Rm | 5-10 | 300-1000 | 300-1000 | 300-1000 | ? | -1000 | ? | ? |
| R/ri | 1-10 | 5-100 | 5-50 | 5-50 | -100 | ? | ? |
上記境界条件の差から、第1にリコネクション速度が各装置で大きく異なってくる。Outflow 速度が速度に達するのはコイルから切り離されたプラズマを加速できるTS-3/4, SSXで、コイルが磁気軸にあるMRXは最大でも速度の3割程度にとどまり、VTF等磁力線が導体に交わる固定境界条件の実験もかなり遅いものと思われ る。反面、リコネクションが遅ければ、室内実験で使われる磁束量に大きな差がないことから、より定常性の高い(dB/dt=0)リコネクションが実現でき る利点がある。第2に各実験装置のバルクプラズマの磁気レイノルズ数Rmも差があるが、オープン系のCS-3を除けば概ね合体を用いた実験は300-1000の中に入る。VTFは、1017-1018m-3の 低密度プラズマを高周波加熱するコンセプトで、最もcollisionlessな実験となることを目指している。第3にこうした合体プラズマの問題点であ るが、装置中の中性粒子の影響に配慮が必要である。例えば、MRXをはじめとするいくつかの実験は電子温度が低く(最低3-5eV)、プラズマは完全電離 していない状況である。特に、トカマク以外の運転モードを用いると中性粒子の影響を生じる場合が多い。リコネクション領域の電子のエネルギー損失が極めて 大きく、電子の加熱や輸送や抵抗等を議論するには問題も想定されるのが現状である。
3.トーラスプラズマ合体を用いた磁気リコネクション実験
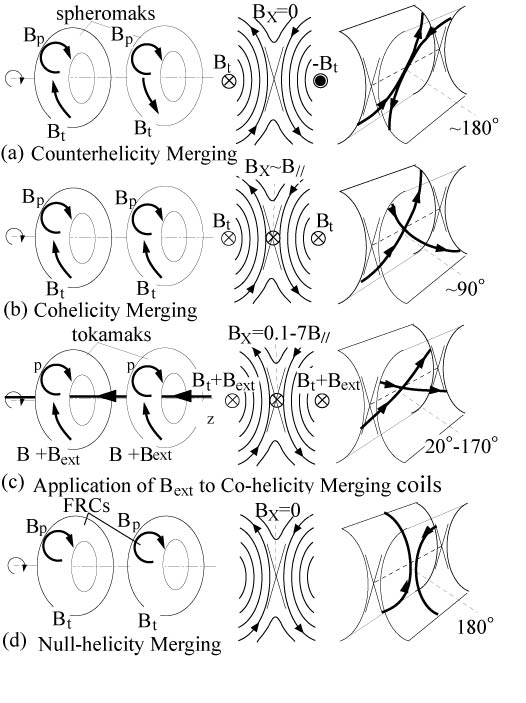
図3のように同方向のトロイダル電流を持つ2つのトーラスプラズマを近づけると、電流同士が引き合って、磁気リコネクションを通じて一つに合体する。その際、(1) 同極性合体と異極性合体を比較する方法、(2) 同極性合体に外部トロイダル磁場を印加する方法により、Xポイントに3成分(2.5次元)磁場構造を持ち込んだ。(1)ではスフェロマックやスフェレータ の軸対称合体時、それぞれのトロイダル磁場の極性を同方向(同極性合体)、逆方向(異極性合体)とすると、図3(a)(b) に示すように磁力線が磁気中性面でそれぞれ約90゜、180゜で交わってつなぎかわることを利用する[6]。
Fig. 3: 2.5-D structures of reconnection regions with third field component BX: (a) counterhelicity merging spheromaks with BX≈0, (b) cohelicity merging spheromaks with BX≈B//, (c) cohelicity mergings of RFPs, spheromaks and tokamaks with varied BX and (d) null-helicity merging of spherators with BX≈0
別の見方をすれば、同極性合体では紙面に垂直(電流シートに平行)な方向の磁場成分BXがつなぎかわる磁場成分B//と ほぼ同一であり、異極性合体ではこれが零となって単純な2成分磁場のみのリコネクションとなる。(2)の合体に使用するトーラスプラズマは、q値(磁力線 がポロイダル方向に1周する間にトロイダル方向を回る回数)の高い方から、トカマク、スフェロマック、逆転磁場ピンチ(RFP)で、つなぎかわるポロイダ ル磁場成分を一定に保つと、Xポイント付近の磁力線同士の角度はq値が大きいほど小さくなる。すなわち、外部から印加するトロイダル磁場は、図3(c)の 磁場成分BXとなり、B//との比は、合体プラズマのq値が大きいほど大きい。この手法の利点は、(1)と異なり磁力線のBX/B//比を連続的に変化できること、さらにBX、B//を 独立に設定できることである。また、フラックスコア電流を用いることによりスフェレータ同士の合体を行い、運転によってはトロイダル磁場成分が少ない Null-Helicity(図3(d))の合体も行われている。以下に、こうした合体を用いて、磁気リコネクションのキーとなる問題がどこまで明らかに されたのか順々に見ていくことにする。
4.磁気リコネクションの縦磁場効果
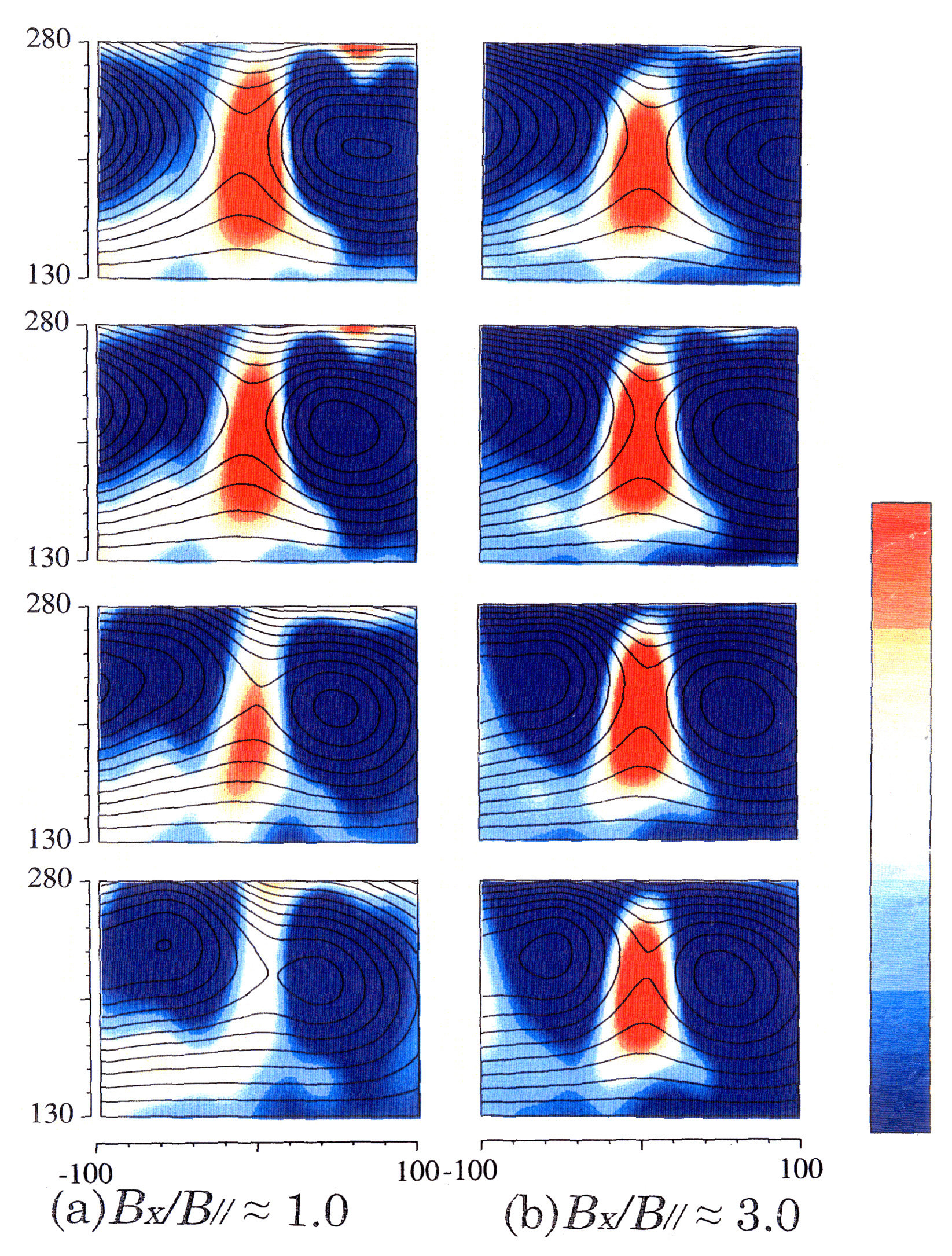
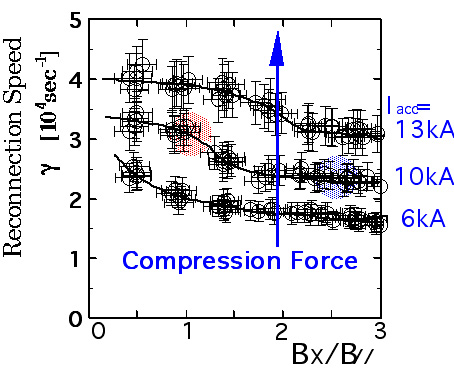
プラズマ合体を用いた磁気リコネクション実験で最初の注目点は、磁気リコネクションそのものが実験室で再現できること、そしてそれが縦磁場BXに対していかに依存するかを検証することであった。例えば、地球磁気圏の昼側で地球磁場と宇宙磁場の交わる角度に対するリコネクション速度の依存性が検証可能である。2種類の外部トロイダル磁場BXに ついて求めたポロイダル磁気面とトロイダル電流密度分布の時間変化(TS-3の2次元磁気プローブデータより)を図4(a)(b)に示す[6,12]。ど ちらの場合もポロイダルコイルの電流波形は同一で、2個のプラズマを押しつける力は一定である。各図の下辺が中心対称軸にあたる。まず、左右からそれぞれ 1個ずつのスフェロマックプラズマが生成されて、いずれの場合も左右から磁力線が近づいてつなぎかわり、共通磁束となった磁力線が上下に流れていく様子が よくわかる。正方向(スフェロマックのトロイダル電流の方向)の電流密度を青で、逆方向のそれを赤で大きさに従って表示したトロイダル電流密度分布を見る と、X点付近にスフェロマックのトロイダル電流と逆向きのシート状の電流、即ち、電流シートが確認できる[6,12]。BX/B//=3の場合は磁気軸は最後まで2個存在するのに対し、BX/B//=1の場合はt=25µsecまでにほぼ9割合体が完了している。2つの場合の合体時間の差は5割程度である。この効果を縦磁場BXを連続的に変化させて検証した結果を図5に示す。リコネクション率は、全体のポロイダル磁束に対するつなぎ変わった磁束の割合(reconnection ratio a)の時間成長率g=da/dt/aで表しており、図4(a)(b)は図5では赤印、青印にあたる。縦磁場BXが増えるほどリコネクション率が低下していることがわかる。同様の効果は、異極性合体と同極性合体を比較しても [6]、MRX実験でも確認されている[7]。問題はなぜ、縦磁場がリコネクション率を低下させるかであるが、後述のイオン運動効果に加え、縦磁場の存在により電流シートの圧縮性が大きく低下することが考えられる。
Fig. 4: 2-D contours of poloidal flux surfaces and toroidal current densities for merging spheromaks with BX/B//≈1 (a) and those for merging tokamaks with BX/B//≈3 (TS-3) [12].
Fig. 5: Dependence of reconnection rate γ on BX component and external compression force Iacc (acceleration coil current) (TS-3) [17].
5.磁気リコネクションは駆動型、自発型?
スフェロマックの両側に設置された外部コイルにスフェロマックのトロイダル電流と逆向きの電流Iaccを流すことによって、合体を加速した場合のリコネクション率の変化は図5のgのIacc依存性を見ればよくわかる。外部力によって合体プラズマを押しつけると磁気リコネクション率が増加する。Iacc=13kAの場合のリコネクション率はIacc=6kAの場合のそれの約2倍に達する。これは磁気リコネクション速度がX点の状態によってではなく、 外部コイル電流という外部条件で決定されることを意味しており、NIFSの佐藤らによって提唱されてきた駆動型磁気リコネクションモデルの妥当性を示している[6]。興味深い点は、Viが 速いほど電流シート層の幅δが小さく圧縮されて高い電流密度が達成されて、電流シートの実効抵抗率が高くなっていることである。結果として、大きな外部力 に対して磁気リコネクションが速く進むようXポイントの実効抵抗が大きくなる一種の自己調整機能を有していることは注目に値する。見かけ上、駆動型に見え る磁気リコネクションを決定しているのは電流シートの異常抵抗という内部要因である。
6.電流シートの異常抵抗と粒子運動効果
問題は、4.や5.で見られた効果がいかなる理由によって生じるかであるが、このような成長率の違いを生じる原因を、イオンラーマー半径と電流シート幅との関連から検証してみる。
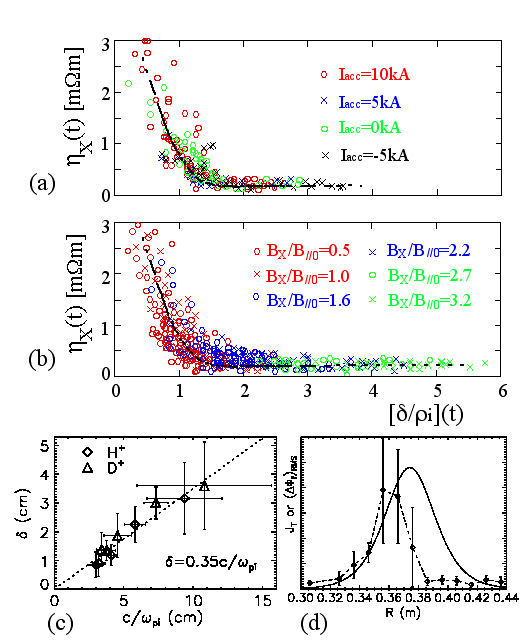
Fig. 6: (a)(b) Time evolutions of effective current-sheet resistivities ηX as a function of current sheet thickness d normalized by ion gyroradius ρi when four different acceleration-coil currents Iacc (a) and six different BX fields (b) are applied to the merging toroids (TS-3) [12,17]. (c) dependence of current sheet thickness d on ion skin-depth c/ωpi and (d) time evolutions of sheet current and electrostatic fluctuation signal at neutral sheet (MRX) [14].
電流シート幅とイオンラーマー半径との関係をより直接的に捉えるために、縦軸に実効抵抗率hXを、横軸にイオンラーマー半径riで規格化した電流シート幅dをプロットしたものを図6(a)(b)に示す(TS-3実験)。(a)は外部圧縮力Iaccを変化した場合、 (b)はBX/B//を変化した場合、それぞれ十数ケースのhX、d/riの時間発展を同じグラフ上にプロットした。イオンラーマー半径はX点における磁場(トロイダル磁場BX) とイオン温度(ドップラー幅より計測)から算出した。興味ある点は、(a)(b)共に電流シート幅がイオンラーマー半径よりも大きいうちは、Xポイントの 実効抵抗率は古典抵抗の2倍程度で一定なのに対し、イオンラーマー半径よりも小さくなると、Xポイントの実効抵抗率の急上昇することである。これは、BX/B//、 Iaccのどちらを変化させてもすべてのデータが一つの線上に一致する。図4(a)の場合にはリコネクション過程において、電流 シートが急激に圧縮されてイオンのラーマー半径以下の幅に狭められて、異常抵抗を生じ、結果的に速いリコネクションが発生している。図4(b)のように大 きな外部トロイダル磁場の影響でイオンは小さい半径のラーマー運動を行う場合は、電流シートの幅はイオンラーマー半径よりも常に大きく、実効抵抗率はほぼ 一定の小さな値となっている。このように、電流シート幅がイオンのラーマー半径付近に低下するため生じる異常抵抗(不安定による電子の散乱)が、 前述のリコネクションの縦磁場効果や外力依存性を実現させているものと考えられる。即ち、電流シートを圧縮する力を大きくすれば、電流シート幅はその分圧 縮されてイオンラーマー半径以下となってリコネクション速度は増加し、またBX成分が小さくなると、イオンラーマー半径が増加するために電流シート幅をそれ以下に圧縮することが容易になって、やはりリコネクション速度は増加するといえる。MRXでは極めて遅いインフロー(TS-3の1/3以下)で準定常なリコネクションを20µsec 程度実現して、この過程を検証している。図6(c)に示すように、準定常期間でシート幅がイオンスキン長(β値が1程度なので、ほぼイオンラーマ半径に等 しい)程度に落ち着くことを計測している[14]。シート幅がイオンラーマ半径を下回ると損失が増えることから、この付近が安定なシート幅になるものと考 えられる。
この効果に関してさらに踏み込んだ微視的なメカニズムについては、現在、第5章に示すようないくつかの説が唱えられている。イオンラーマー半径以下に電流シート幅が圧縮されると、もはやMHD 近似としての電流シートという概念は成り立たず、イオンは電流シート内に拘束されず、その外でメアンダリング運動を行うことになり、さらに電流シート内に はlower hybrid drift instability(LHDI)等の不安定性が誘起されると考えられる。MRXではこの異常抵抗と不安定の関係を検証中である。図6(d)にLHDI と考えられる電流シート内の揺動を捉えた例を示す[14]。シート電流が形成される時間帯にelectrostaticな揺動が成長していることがわか る。ただ、現在のところ、異常抵抗との時間的な相関が見られず、異常抵抗とは別の現象ではないとの見方をとっている。
7.磁気リコネクションのエネルギー変換効果の検証
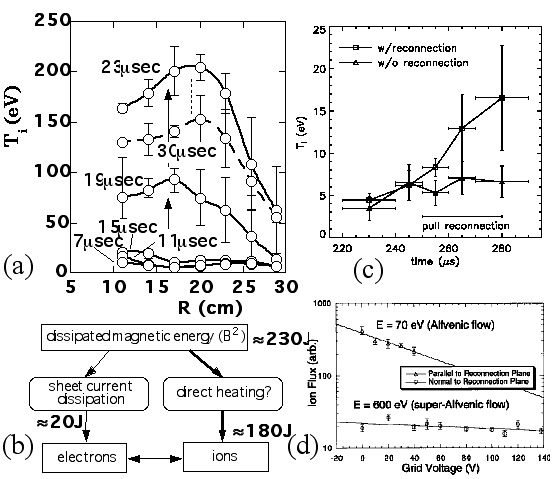
太陽フレアで放出される膨大な運動・熱エネルギーに代表される磁気エネルギーの解放過程はリコネクション研究の中心課題である。Sweet- Parkerモデルに従えば、最も重要なエネルギー変換過程は、上流側の磁気エネルギーが電流シートの抵抗損失として熱エネルギーに変換される過程と考え られるが、近年の太陽コロナの磁気リコネクションでは、電流シートの拡散から見積もった加熱エネルギーは実際に観測されるプラズマ温度を説明するにはあま りに小さいことがわかってきた。代わって注目され始めたのは、磁気リコネクション点の下流側で生じるプラズマ粒子加速によるエネルギー変換である。実験に よってこうした粒子加速効果や加熱効果、エネルギー変換効果を検証することができるであろうか。TS-3でBXが零の最も基本的な リコネクションとなる異極性合体でイオン温度を計測してみると、イオンのみが選択的に加熱される現象が発見された。図7(a)に、ドップラー幅法で測定し たイオン温度の径方向分布を示す[15]。初期にイオン温度は一様に10eVと低温であるが、合体と共に(t=10µsec)に急上昇を始め、合体が終了する10µsec 以内に最大200eVに到達している。電子温度は10eVから20eVの間で大きく変化しないため、これはイオンのみの選択的加熱現象といえる。図 7(b)に示す磁気リコネクション過程のエネルギーフローを見るとイオンの熱エネルギーの上昇は180Jと計算され、これは合体プラズマの磁気エネルギー 減少分230Jの約80%に達することが判明した。一方、Xポイント領域の電流シートの抵抗損はわずか20Jと少なく、イオン熱エネルギー上昇分に比べて 遥かに小さい。これは電流シートの抵抗損によるプラズマ加熱の古典的イメージと大きく異なる。消滅した磁気エネルギーがアウトフローを通じてイオンの熱エ ネルギーに変換されたと結論される[15]。電流シート内の局所的なイオン・電子温度の計測はMRXでも行われ、図7(c)にその結果を示す。上記アウト フローによるイオン加熱に比べるとかなり低いが、イオン温度が17eVまで加熱され、リコネクションのない場合の5eVに比べて高いことがわかる。これは 異常抵抗そのものを発生させる不安定がイオン加熱にも貢献していることを示している[16]。さらにSSX実験では、図7(d)に示すようにアウトフロー 中に速度を大幅に越える速度成分を有する高速粒子が存在していることが報告しており、議論になっている[8]。
Fig. 7: (a) Radial profiles of ion temperature and (b) energy flow during counterhelicity reconnection of two spheromaks from t=5µsec to 20µsec (TS-3) [15], (c) time evolutions of ion and electron temperatures of two spherators with and without magnetic reconnection (MRX) [16] and (d) super Alfvenic flow of merging spheromaks measured by ion energy analyzer (SSX) [8].
8.プラズモイドの発生と間欠リコネクション
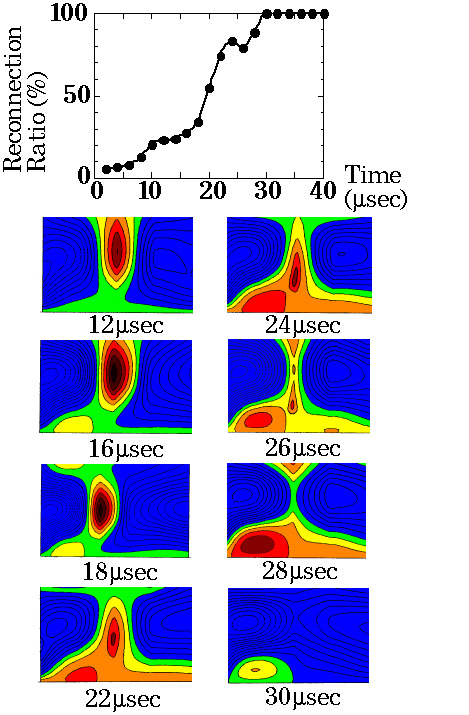
では、異常抵抗でも賄いきれない大きなインフローがある場合、あるいは異常抵抗の効果が少ないMHD 領域ではリコネクション速度は単に電流シート抵抗によってその上限が決められるのであろうか。TS-3では、2重に配置された外部圧縮コイルを使用して トーラスプラズマを外部から強く押しつける実験を行い、結論として電流シートの間欠放出現象を見出している。図8下図ではトロイダル電流密度を正方向(合 体プラズマのトロイダル電流の方向)の電流密度を大きさによらず青で、逆方向のそれを大きさに従って緑から黄色さらに赤で表示した。コイルによりインフ ローが極めて大きく駆動されるため、磁力線はパイルアップし、電流シートは図8に示されるように次第に円形に変形していく。そして間欠的に電流シートが放 出されることが判明した。TS-3で作られる磁束の範囲で最大2回のシート放出が観測されている。興味ある点はこの電流シート放出現象が間欠的発生がリコ ネクションの高速化を引き起こす点で図8上では放出時に合体率reconnection ratio aが急増していることがわかる[12]。 この時、電流シートと共にプラズマ粒子も排出され、結果的にMass Ejectionが促進される形で高速リコネクションが発生していることが最近の密度計測からも確かめられている。高速リコネクションの一つの形態は非定 常・間欠リコネクションであることが示唆される。
Fig. 8: Current sheet ejection observed in 2-D contours of toroidal current density (lower) and time evolution of reconnection ratio a (reconnected flux / total flux) (upper) (TS-3) [12].
9.理論モデルとの照合
室内実験を用いて古典的な理論モデルの検証を試みることも徐々に可能になってきている。定常モデルと比較を行う際、障害となっているのはリコネクションと共に磁場構造が変化し、下式の左辺dB/dtが零にならないことであった。
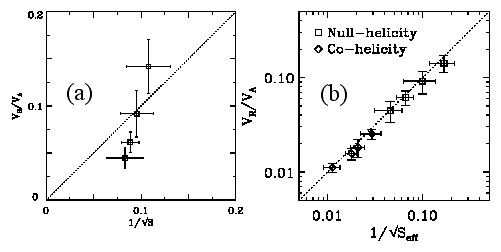
MRXではその特徴であるゆっくりとしたインフローを利用して、dB/dt=0の状態を20µsec程度作り、定常リコネクションのSweet-Parkerモデルの証明を行っている[13]。一般に時間で規格化したリコネクション速度Viは、、のように磁気レイノルズ数の1/2 乗に反比例する。dB/dt=0だけでは、図9(a)のようにモデルに合致しないため、(1)電流シートの異常抵抗、(2)さらに電流シート内の圧力の時 間変化(非定常効果)を考慮するなど、Sweet-Parkerモデルを一般化する必要があることが判明した。図9(b)に、速度で規格化したリコネク ション速度と(1)(2)の効果に基づいて修正した後の磁気レイノルズ数との関係を示す。一般化により、磁気レイノルズ数の1/2乗に比例するリコネク ション速度を得て、モデルと合致することを報告している[13]。この結果はいくつかの示唆を与えている。即ち、Sweet-Parkerモデルでリコネ クション速度を説明する上で電流シートの異常抵抗や電流シートの圧力分布が重要であること、そして定常のリコネクションを実現しようとしても、実際には シート内の粒子蓄積が徐々に進行するなど圧力変化が生じて定常モデルの実現がなかなか難しいことである。
Fig. 9: Dependences of reconnection inflow normalized by Alfven speed on magnetic Reynolds number S before (a) and after (b) the correction of Sweet-Parker model (MRX) [13].
10.まとめ
磁 気リコネクションは、すべての磁化プラズマの磁場構造変化を理解するための要素物理として、現在、再び実験研究が盛んになりつつある。プラズマ合体を用い た磁気リコネクション実験は、「Xポイント」という「特定の場所」の「特定の物理」を抜き出して検証する専用物理実験が成立する可能性を示したものといえ る。通常とは逆に、プラズマ閉じ込め実験を「磁気リコネクション」というプラズマ物理の解明の道具として利用した実験ともいえよう。実験室プラズマは、人 為的にプラズマが制御でき、しかも計測の自由度も最も大きい長所を有している。従来、問題であった温度密度の確保や境界条件も、クローズ系実験の登場によ りある程度の解決が可能となった。実験グループ数もこの数年で7、8に急増し、磁気リコネクション現象の解明のためのパワフルなツールとして期待を集めて いる。今後の課題としては、1)放射損失やプローブの挿入等による電子のエネルギー損失の低減、2)一部の運転で見られる中性粒子の影響の低減、3)プラ ズマに影響を与えない多次元・高空間分解のプラズマ計測法の開発などがあげられる。現在、室内実験は、衛星観測、理論、計算機シミュレーションの3つの分野と相互連携する動きが本格化しつつあり、こうした分野を越えた協力が順調に拡大すれば、磁気リコネクションの解明に大きな貢献が期待できよう。
参考文献
[1] S. Masuda et al., Nature 371, 495 (1994).
[2] T. Shimizu and S. Tsuneta et. al., Astrophys. J. 422, 906 (1993).
[3] N. Ohyabu et al., Phys. Fluids 17, 2009 (1974).
[4] R. Stenzel and W. Gekelmann, J. Geophys. Res. 86 , 649 (1981); ibid. 87, 101 (1982); W. Gekelman and H. Pfister, Phys. Fluids 31, 2017 (1988).
[5] A. Frank et al., Contrib. Plasma Phys. 36, 667, (1996).
[6] Y. Ono et al., in Proc. IEEE Int. Conf. Plas. Sci., (Saskatoon, 1988) p.77;小野 靖等,プラズマ・核融合学会誌 56, 214 (1986); 桂井 誠等,電気学会論文誌 107A, 65 (1987);M. Yamada et al., Phys. Rev. Lett. 65, 721 (1990); Y. Ono et al., Phys. Fluids B5, 3691 (1993).
[7] M. Yamada et al., Phys. Plasmas 4, 1936, (1997).
[8] M. Brown, Phys. Plasmas 6, 1717, (1999).
[9] J. Egedal and A. Fasoli, Phys. Rev. Lett. 86, 5047, (2001).
[10] L. W. Jones, Private communication.
[11] J. Yee and P. M. Bellan et al., Phys. Plasmas 7, 3625,(2000).
[12] Y. Ono et al., Phys Plasmas 4, 1953, (1997).
[13] H. Ji et al., Phys. Plasmas 6, 1743, (1999).
[14] M. Yamada et al., Earth, Planets and Space 53, 509, (2001).
[15] Y. Ono et al., Phys. Rev. Lett. 76, 3328, (1996).
[16] S. Hsu et al., Phys. Rev. Lett. 84, 3859, (2000).
[17] Y. Ono et al. Earth, Planets and Space 53, 521, (2001).